学科建设
- 数学学科
应用数学、概率论与数理统计、数学与交叉学科三个学科方向建设。
①应用数学学科介绍:
以数学分支的应用基础为核心,同时解决自然科学、工程技术、信息科学、经济和管理等领域中的数学问题。通过建立数学模型和应用数学方法,应用数学为科学与技术的创新提供了重要支撑。
该学科的研究方向主要包括:非线性偏微分方程,发现新的处理非单调、非凸不可微能量泛函的方法;拓扑学及其应用,特色在于结合现代拓扑、微分方程与几何、代数,并利用计算机进行计算或验证;数值方法的研究及其应用,研究优化计算方法、数值线性代数问题,以及约束矩阵方程问题;代数学及应用,研究矩阵几何及应用、环上矩阵论及应用、群论及应用、Clifford代数,Hopf代数及应用,以及代数学在计算机科学与信息科学的应用,可能的突破包括继续保持矩阵几何与矩阵论研究的国内较高水平,并发展新的研究方向。

(F Jurado et al. , 2023, Fractal and Fractional )
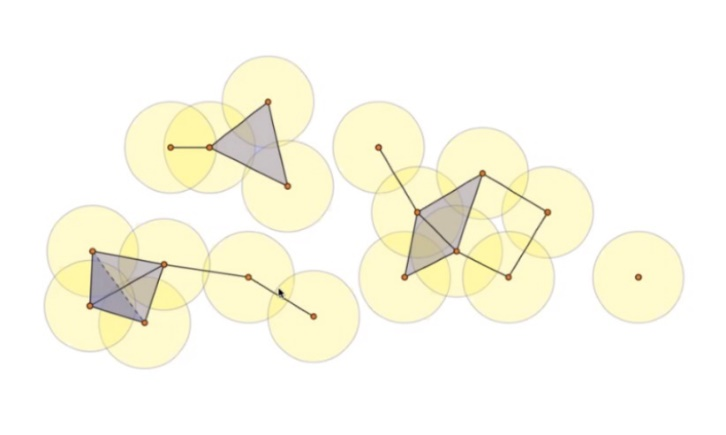
(Otter, N. et al., 2017, EPJ Data Science)

(Valencia-Ponce MA et al., 2021, Mathematics.)
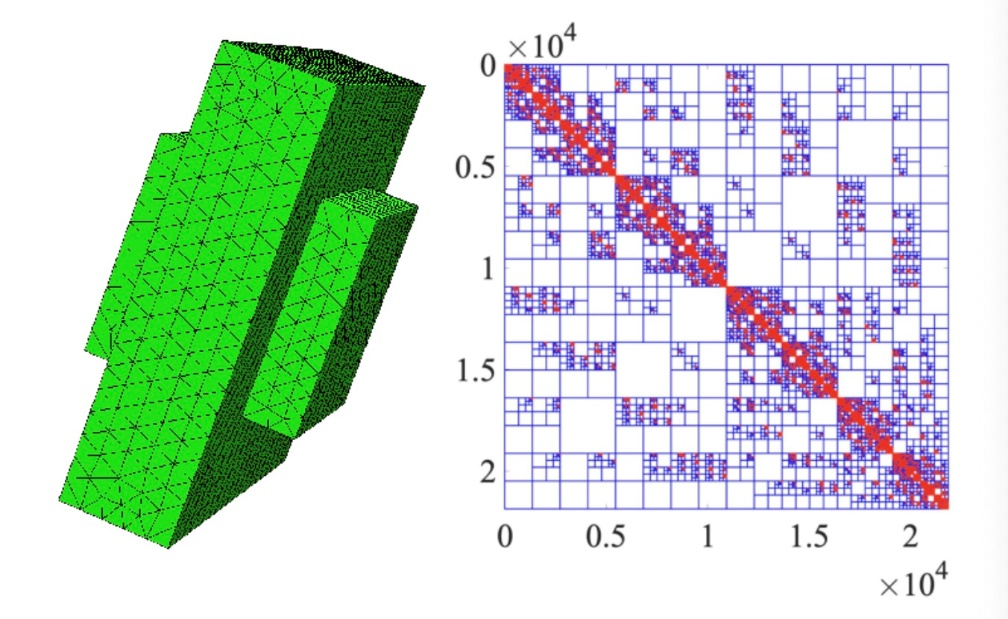
(Parvizi, M.et al.,2022, In International Conference on Domain Decomposition Methods)

(Wang, C. et al.,2024,In International Conference on Medical Image Computing and Computer-Assisted Intervention )
②数学与交叉学科介绍:
数学与交叉学科是数学与其他学科(如物理学、化学、生物学、医学、计算机科学、经济学、工程学、社会科学等)深度融合的领域。数学通过提供严谨的理论框架、抽象思维方法以及高效的计算工具,成为连接不同学科、解决复杂问题的桥梁。在交叉学科中,数学的应用范围极为广泛,包括但不限于建模、仿真、优化、数据分析、预测和理论推导等方面。例如,数学为物理学提供了描述自然规律的微分方程和几何结构,为生物学构建了种群动态模型和遗传算法,为计算机科学、机器学习和密码学奠定了理论基础,为医学人工智能、自动驾驶等算法提供了理论框架等等。与此同时,交叉学科的实际需求也推动了数学理论的发展,催生了诸如动力系统、随机过程、拓扑学、计算数学、医学数学等新的研究方向。数学与交叉学科为其他学科提供了新的视角和方法论支持,成为现代科研与技术创新的重要驱动力。
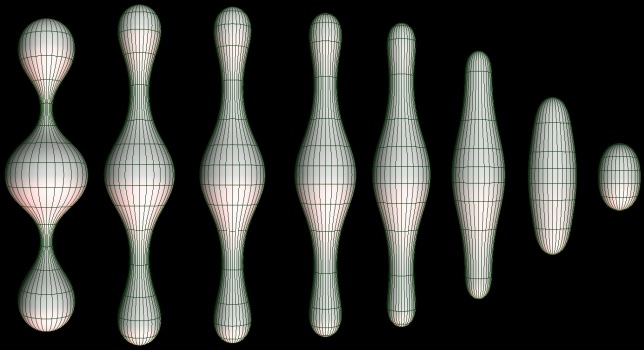


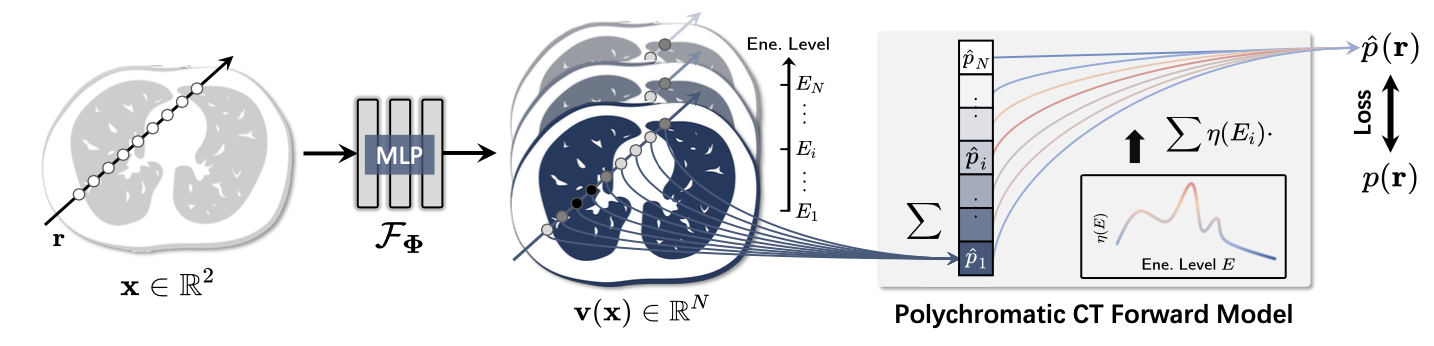


③概率论与数理统计学科介绍:
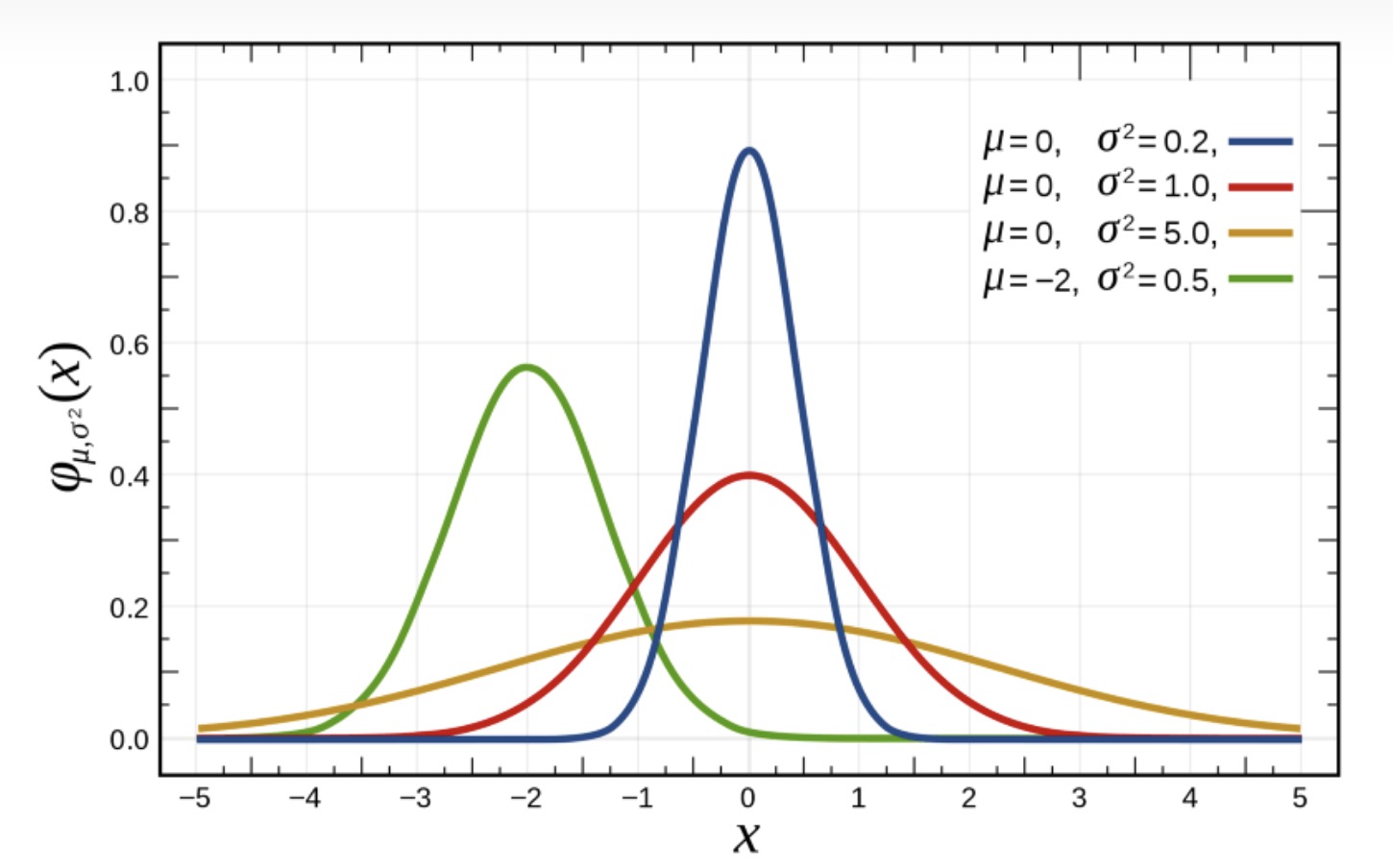
概率论与数理统计是数学的重要分支,是一门研究随机现象的规律性及其数学模型的现代数学学科。概率论侧重于研究随机事件发生的可能性及其规律,而数理统计则基于概率理论,研究如何从数据中推断样本的特点并推及总体特性。这一学科的核心目标是通过数学工具和逻辑推理,从不确定性中提取信息并作出
科学决策,这奠定了该学科在生命科学、信息科学、工程技术等诸多领域的应用。随着人工智能等新领城的发展,该学科也在不断发展并涌现出新的理论和方法,如数据挖掘、复杂系统建模等,这些新领域为该学科的进一步发展提供了新的动力和方向。
我院该学科的研究方向主要包括:随机过程,针对不同准则下的马氏决策过程(Markov Decision Processes),寻找最优策略的存在性条件及其算法;博弈论,特别针对零和及非零和的随机博弈(Stochastic Games),证明纳什均衡策略的存在性条件及其算法;随机过程及博弈论中理论构建,主要基于存在性证明所得结论,并结合实际例子对理论进行阐释;极限理论,着重于研究概率分布的极限性质;人工智能与现代博弈理论,主要结合人工智能算法来制定最优策略;统计机器学习及其在医学影像中的应用,结合统计分析方法和特征选择技术,找到针对疾病诊断更有效的特征,减少冗余数据信息并提高算法效果。



- 物理学科
开展粒子物理与原子核物理、理论物理、等离子体物理和光学四个学科方向建设。
①粒子物理与原子核物理学科介绍:
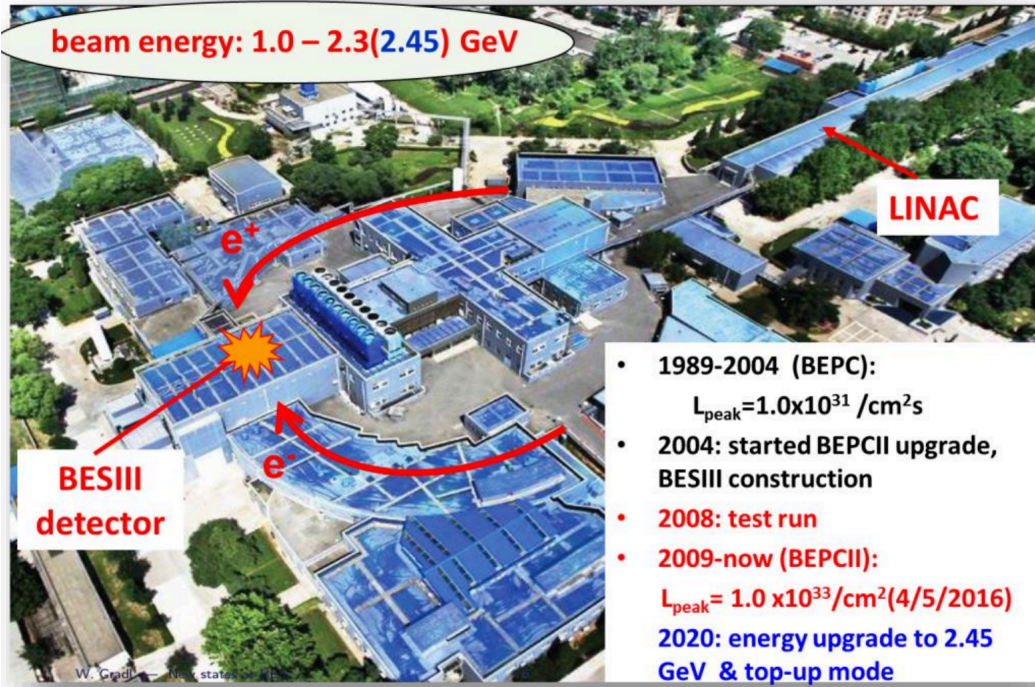
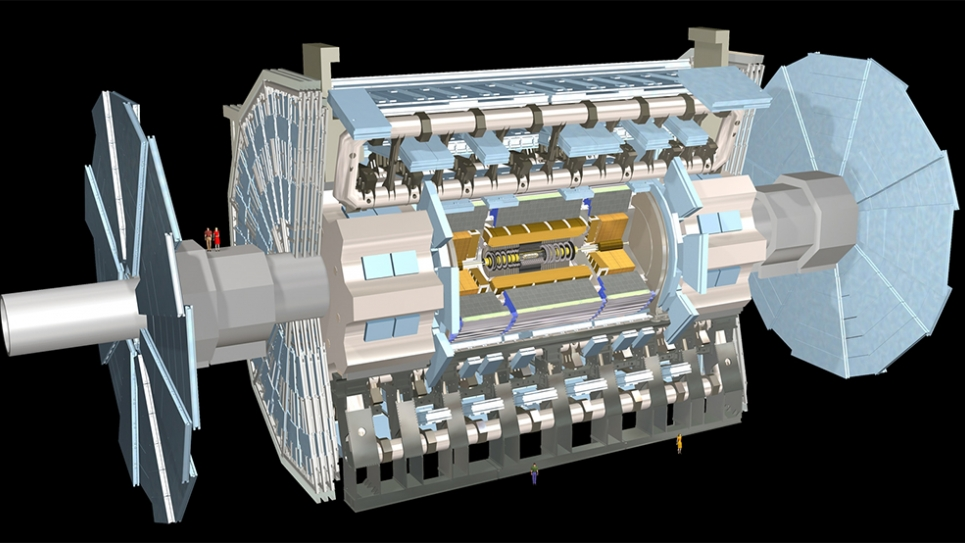
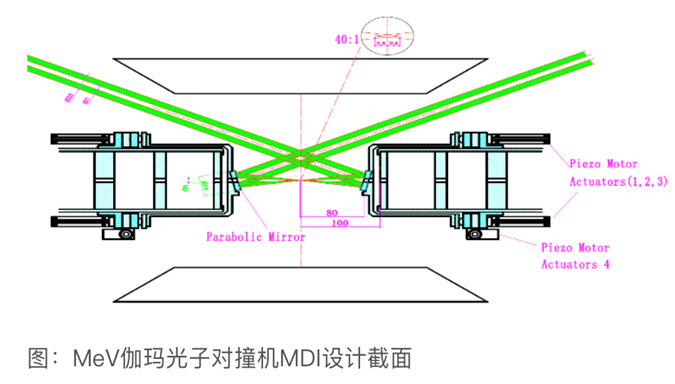
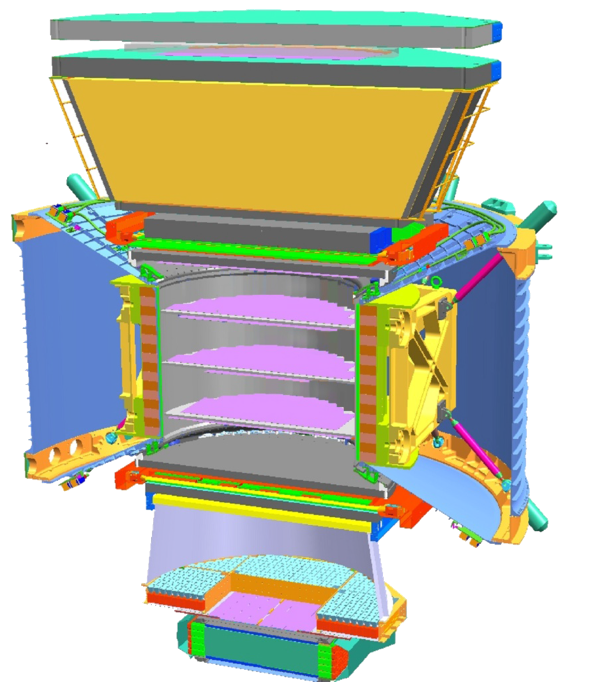
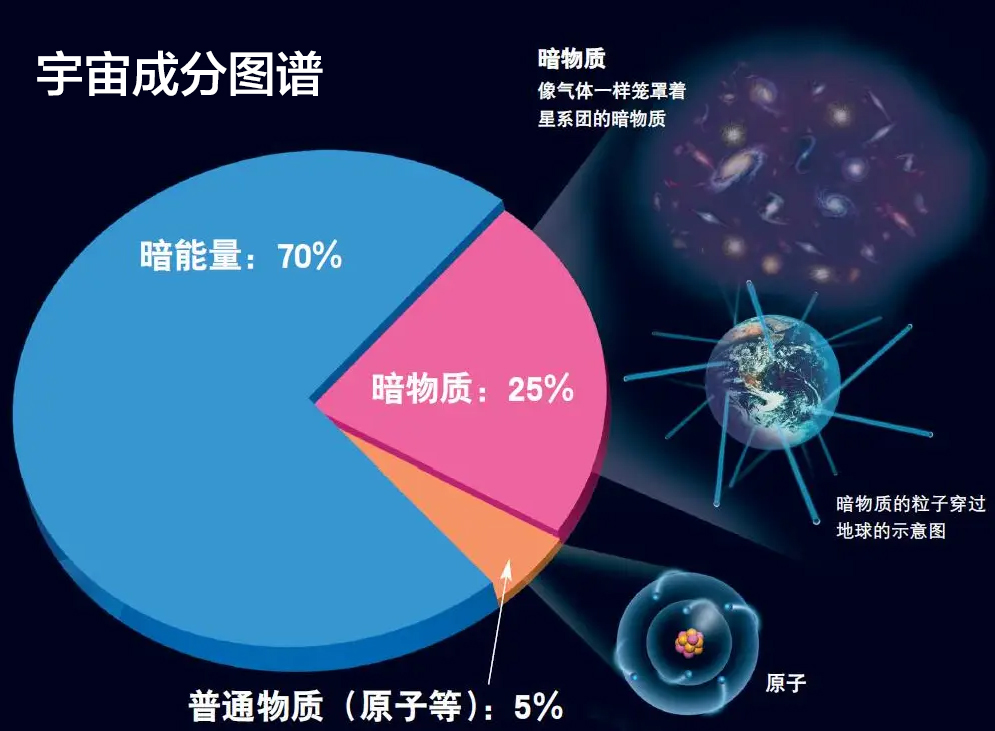
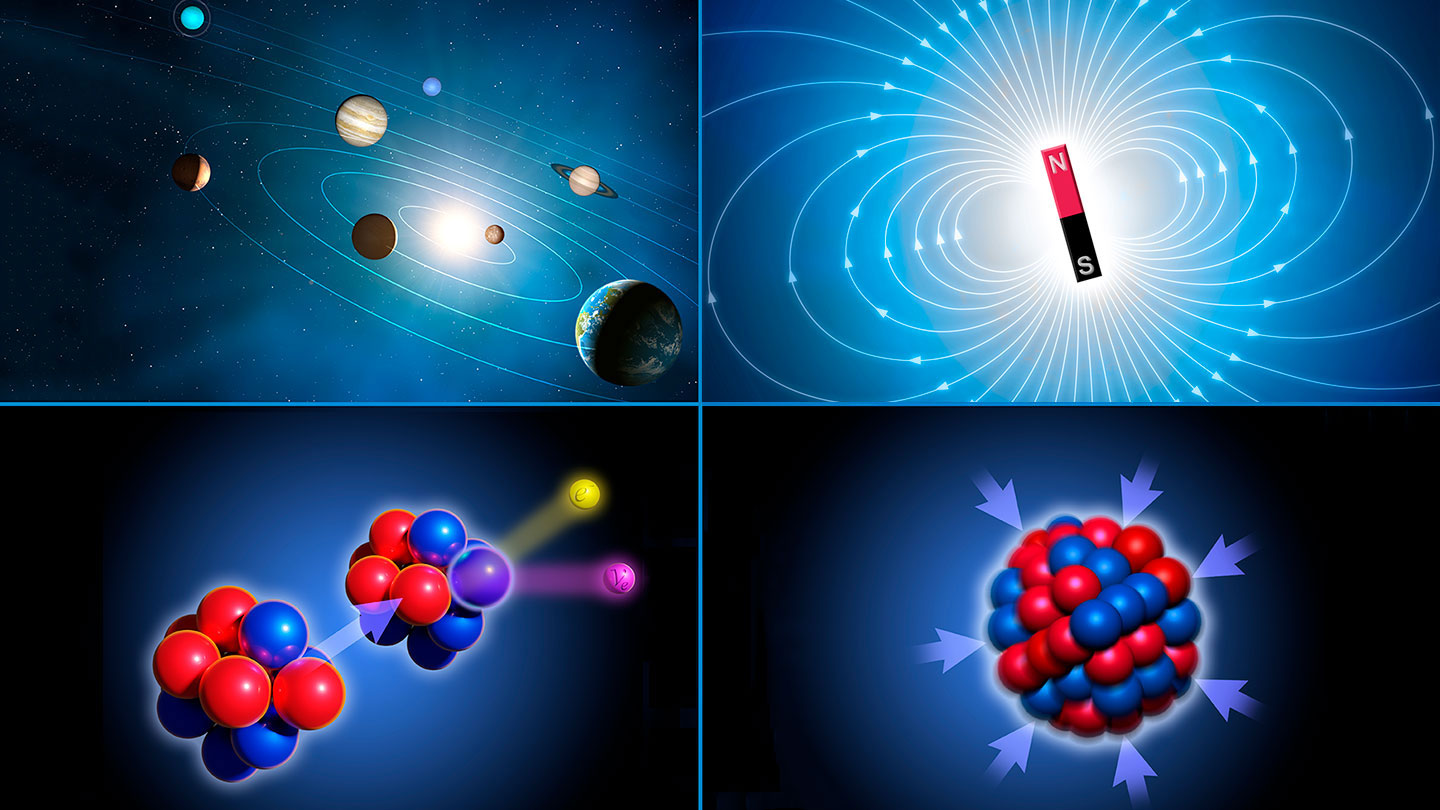
粒子物理与原子核物理致力于探索微观物质结构及其相互作用,揭示质量的起源、时空的本质等自然科学中的基本问题。主要研究方向包括:高能物理实验,粒子物理现象的理论研究,新型探测器及新探测技术,高能物理软件和计算技术,机器学习在高能物理实验中的应用。在应用方面涵盖了核分析技术,核技术在工业和生物医学中的应用,以及辐射物理与其实际应用等。目前开展的主要研究课题包括研究和建设伽马光子对撞机实验平台,参与ATLAS,BESIII,AMS等国际前沿的粒子物理实验合作,同时参与未来对撞机如CEPC与STCF等实验预研和探索。
大科学装置深入探索物质的内部结构,揭示其最小组成单元及相互作用规律,认识宇宙及其演变规律。学科在宇宙演化、基本粒子及其相互作用、新型物质形态等领域取得了重要突破,并不断推动相关技术的革新,广泛应用于国家安全,能源,医疗,信息等领域。

②理论物理学科介绍:
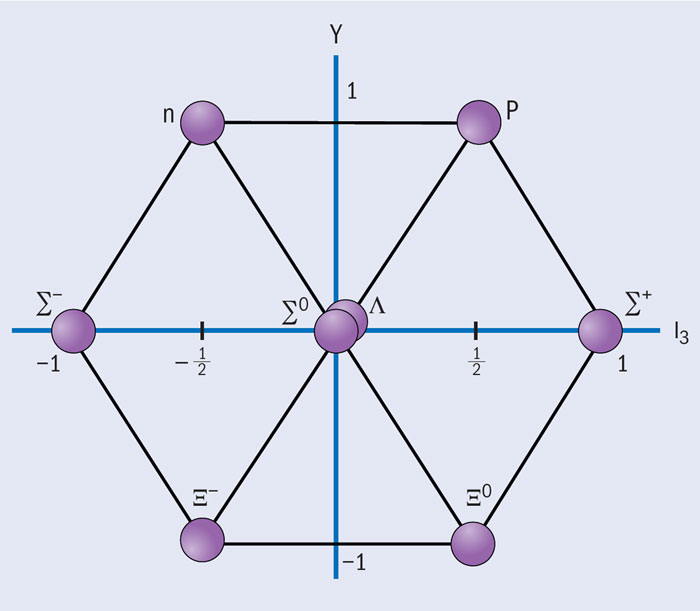
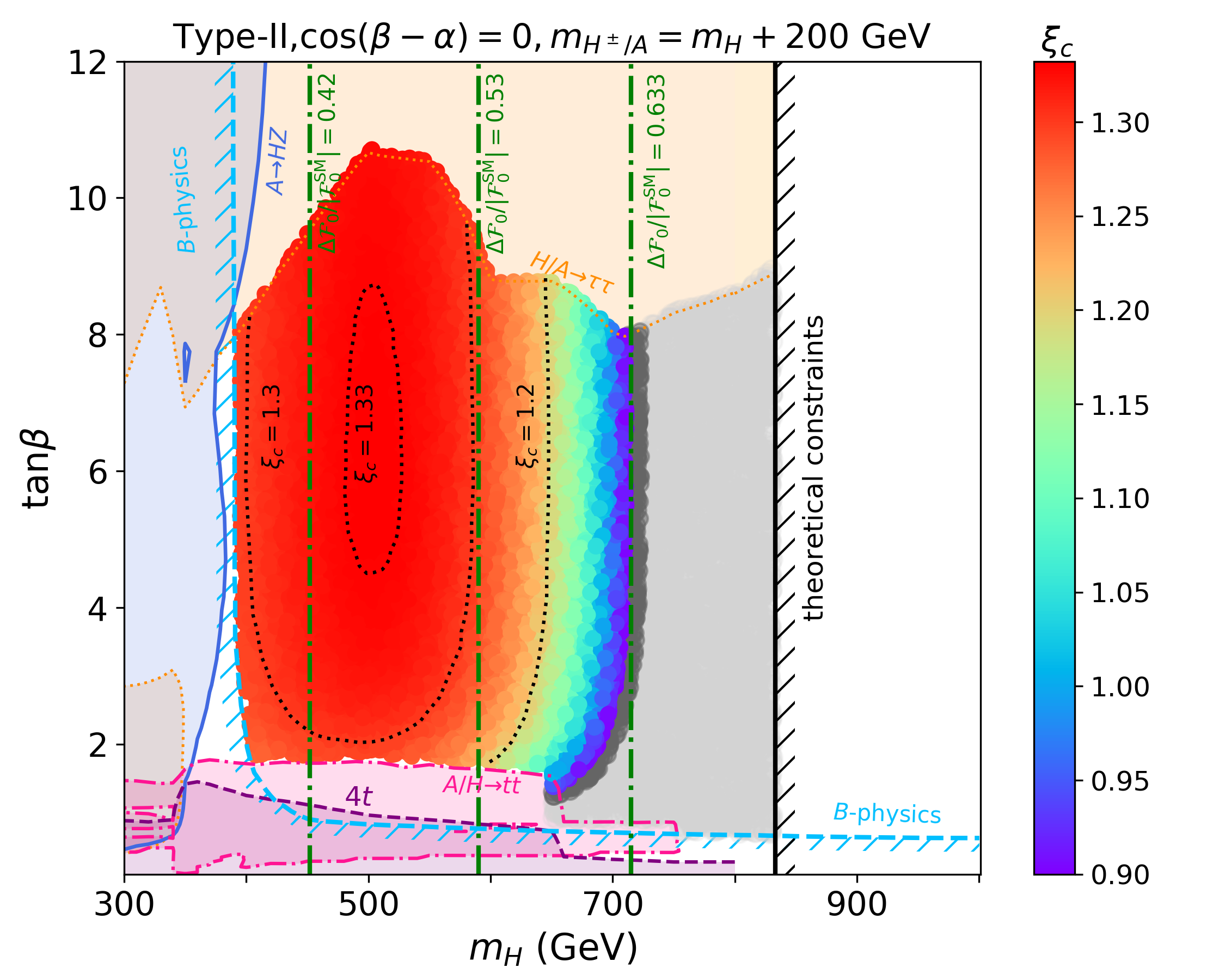
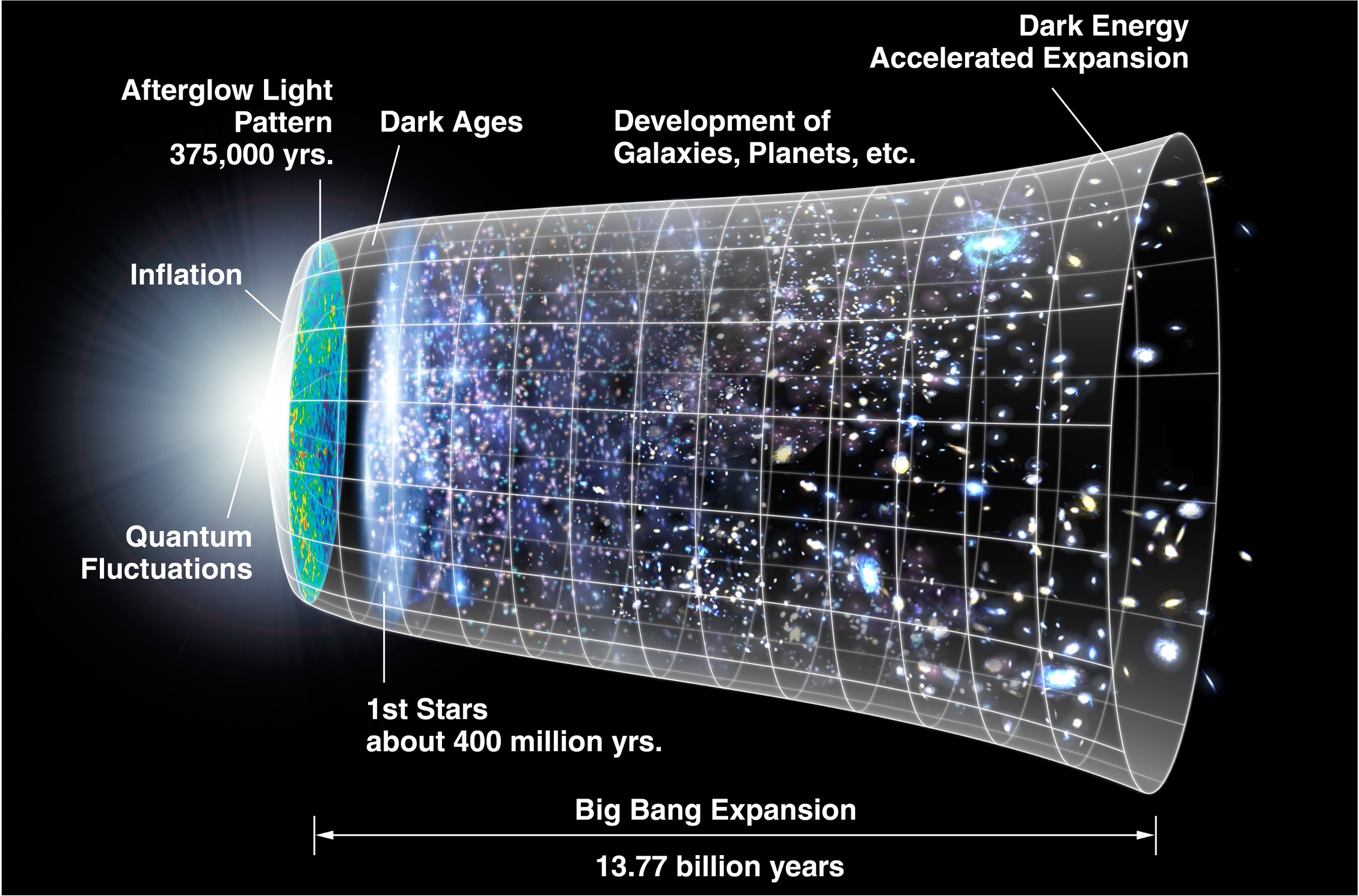
理论物理作为物理学的重要分支,致力于探索自然界未知的物质结构、相互作用和物质运动的基本规律。其领域涵盖粒子物理与原子核物理、凝聚态物理、宇宙学等物理学所有分支的基本理论问题,理解和预言对应的物理现象,是人类探索未知世界的先驱力量。结合学院规划,我院将发展以高能物理理论为核心的理论物理方向,从微现的基本粒子到宏观的宇宙结构理论,连接多种大科学装置和物理前沿实验,并支持和发展多种应用学科基础理论。
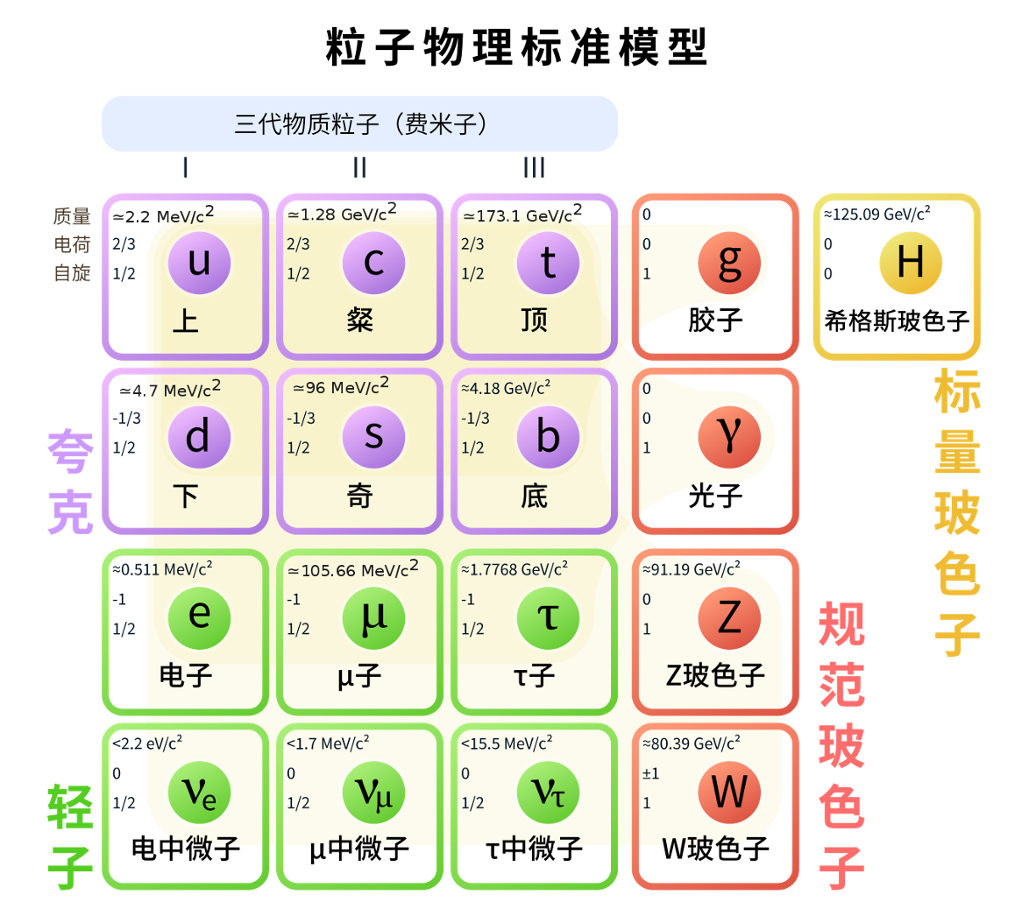
前沿方向之一。
③等离子体物理学科介绍:
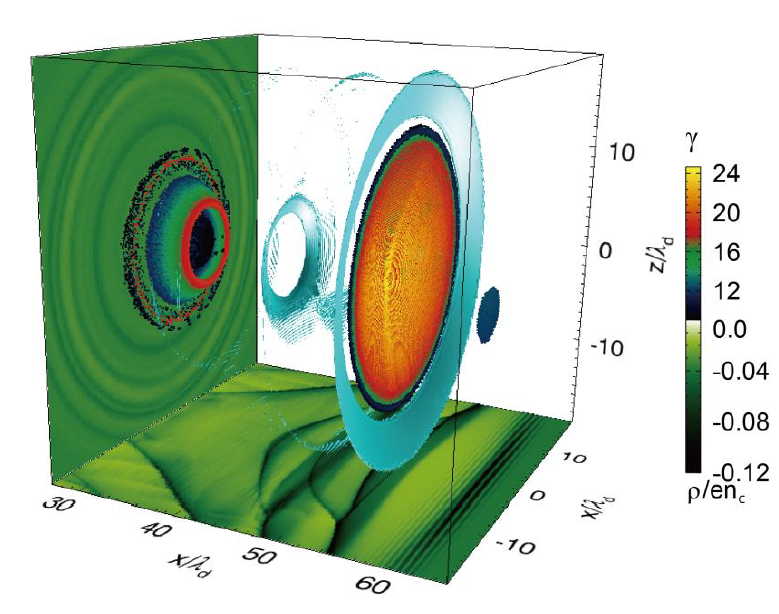
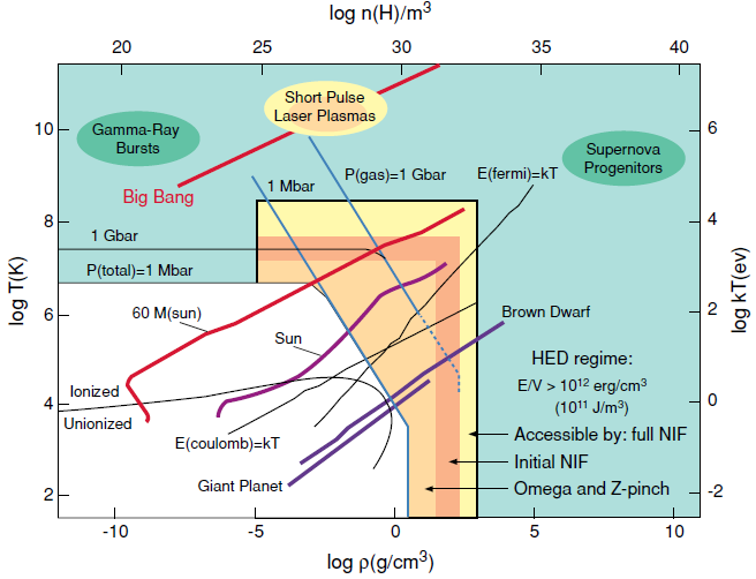
从火焰、闪电到实验室聚变装置(如磁约束、惯性约束聚变装置)、太阳风、日冕等都是等离子体物理的研究对象,研究激光等离子体相互作用以及聚变等离子体的行为特性,探索其物理机制,研究空间科学中等离子体,利用数值计算方法研究粒子加速新原理、等离子体的复杂集体动力学行为等,都是等离子体物理的研究方向。它是一个与国家惯性约束聚变能源大科学工程紧密结合的学科,在国家的能源发展战略、空间研究与开发以及许多先进科学技术领域占有重要地位,具有强烈的应用背景。



④光学学科介绍:
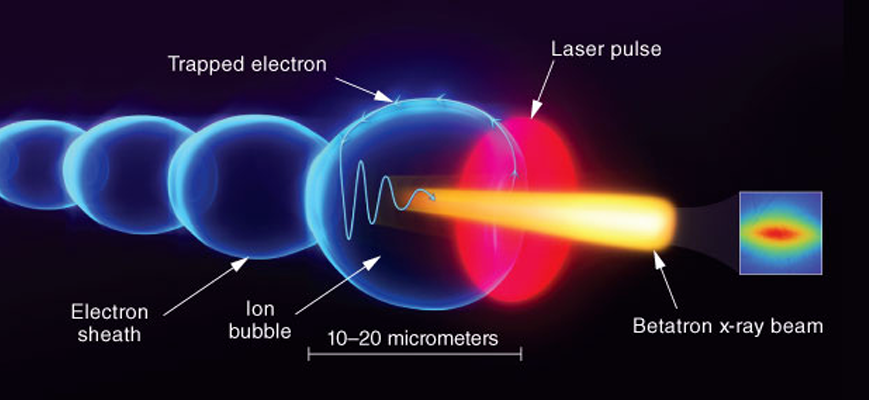
光学学科聚焦超快激光技术、非线性超快光学技术与光学成像技术,致力于引领光学前沿研究和技术创新。学科团队凭借卓越的科研实力,积极参与国家重大科技工程,助力大湾区科学中心建设,推动深圳自由电子激光装置、松山湖阿秒科学中心等重大科研平台的建设与应用。此外,光学学科还参与国家重大科研仪器研制项目,突破多项关键技术,取得了显著科研成果。这些成就不仅为国内外科学技术进步提供了有力支撑,也为相关产业的创新发展奠定了坚实基础。通过持续的技术创新和高水平人才培养,光学学科将持续为国家战略科技发展贡献重要力量。



